8 Ağustos 2010 Pazar
Elektrik ve elektronikte Bizi ilgilendiren Temel kanunlar şunlardır:
1. Ohm kanunu
2. Joule kanunu
3. Kirchhoff kanunu
4. Norton teoremi
5. Thevenin teoremi
OHM KANUNU
Bir elektrik devresinde; akım, voltaj ve direnç arasında bir bağlantı mevcuttur. Bu bağlantıyı veren kanuna Ohm kanunu adı verilir. 1827 yılında Georg Simon Ohm şu tanımı yapmıştır: Bir iletkenin iki ucu arasındaki potansiyel farkının,iletkenden geçen akım şiddetine oranı sabittir.
R = V / I şeklinde ifade edilir.
Burada R dirençtir.
Bu direnç rezistans veya empedans olabilir.
V volttur.
İ de akım yani Amperdir.
Su dolu bir depo olsun, bunun dibine 5 mm çapında bir delik açalım, bir de 10 mm çapında bir delik açalım. Büyük delikten daha çok suyun aktığını yani bu deliğin suyu daha az engellediğini görürüz. Burada deliğin engellemesi dirence, akan suyun miktarı akıma, depodaki suyun yüksekliği voltaja karşılık gelir. Elektrik devrelerinde de, bir gerilimin karşısına bir direnç koyarsanız, direncin müsaade ettiği kadar elektron geçebilir, yani akım akabilir, geçemeyen itişip duran bir kısım elektron ise, ısı enerjisine dönüşür ve sıcaklık olarak karşımıza çıkar. Direnç birimi "Ohm"dur bu değer ne kadar büyük ise o kadar çok direnç var anlamına gelir.
JOULE KANUNU
James Prescott Joule 1818 ile 1889 yılları arasında yaşamış bir İngiliz Fizikçidir. Esasen Isı enerjisi ile Mekanik enerjinin eşdeğer olduğunu göstermiştir ve Joule adı enerji birimine verilmiştir. Bizi ilgilendiren Joule Kanunu şöyledir: Bir iletkenden bir saniyede geçen elektriğin verdiği ısı: iletkenin direnci ile, geçen akımın karesinin çarpımına eşittir
W = R x I2 dır. Esasen formül kalori olarak şu şekildedir:
Kalori = 0.2388 x R x İ x İ x t saniye
Bir kalori 4.1868 Joule eşittir.
O halde Joule = R x İ x İ x t saniye olur.
Güç birimi olan Watt, İskoç mühendis James Watt'tan isim almıştır.
Watt = Joule / saniyedir.
O halde; yukarıdaki formül ortaya çıkar.
W = R x İ2 olur.
Ohm kanununda ki R = V / İ
eşitliğini burada yerine koyarsak, bir formülümüz daha olur:
W = V x İ
KİRCHHOFF KANUNLARI
Gustav Robert Kirchhoff (1824 - 1887) bir Alman fizikçidir. Bizi ilgilendiren iki kanunu vardır.
Bunlar birinci kanun veya düğüm noktası kanunu ile ikinci kanun veya kapalı devre kanunudur.
Düğüm Noktası Kanunu
Bir düğüm noktasına gelen akımların toplamı ile bu düğüm noktasından giden akımların cebirsel toplamı eşittir.
1, 4, 5 nolu akımlar giden,
2 ve 3 nolu akımlar gelen olduğuna göre;
İ 1 +İ 4 + İ 5 = İ 2 + İ 3 olur.
Şekilde görüldüğü gibi, gelen İ akımı giden İR1+İR2+İR3 akımları toplamına eşittir. Burada: R1 =10 ohm R2 = 20 Ohm ve R3 = 20 Ohm olsun, devre gerilimini de 50 V kabul edelim. Devreye gelen İ akımı 10 amper olur ve bu 10 amper lik akım, dirençler üzerinden şu şekilde geçer. İ = V / R olduğundan : İR1 = 5 A İR2 ve İR3 = 2.5 A dır. Böylece dirençler üzerinden giden akımların toplamı da 10 A olur ve gelen ile giden akımların toplamı aynı kalır.
Kapalı Devre Kanunu
apalı bir elektrik devresinde bulunan gerilim kaynakları toplamı ile bu devredeki dirençler üzerinde düşen gerilimlerin toplamları eşittir
Devrede 20 ve 10 V'luk iki gerilim kaynağı mevcut olsun ve ters yönde bağlı olsunlar.Gerilim kaynaklarının toplamı 20 - 10 = 10 volt eder. R1 2 , R2 3 , R3 de 5 Ohm ise, her bir direncin uçlarında düşen gerilim nedir ?
Toplam direnç 10 Ohm olduğu için devreden 1 Amper akım geçer, her dirençten bu akım geçtiği için; V = İ x R den V1 = 1x2 volt V2 = 1x3 volt V3 = 1x5 volt Olur, böylece toplam voltaj düşümleri de 10 V'a eşit demektir.
THEVENİN TEOREMİ
Leon Thevenin (1857 - 1926) bir Fransız fizikçisidir. 1883'de adı ile anılan teoremi ortaya atmıştır.
Buna göre:Doğrusal direnç ve kaynaklardan oluşan bir devre, herhangi iki noktasına göre bir gerilim kaynağı ve ona seri bağlı bir direnç haline dönüştürülebilir; Elde edilen devreye Thevenin;in eşdeğer devresi denir. Bu teoremin bize ne faydası vardır? Faydası şudur: Devrenin herhangi bir kolundan geçen akımı, diğer kollardan geçen akımı hesaplamadan bulabiliriz
Örnek:
Aşağıdaki gibi bir devremiz olsun. Devre no 1 R2 ve R3 3 Ohm R1 ve R4 2 Ohm olsun.V1 gerilim kaynağı 120 Volt , V2 gerilim kaynağı zıt yönde 80 V olsun. Rx direnci 17.5 Ohm ise bu dirençten ne kadar akım geçer?
Bu devreyi ;Thevenin; kuralına göre bir gerilim kaynağı ve buna seri bağlı bir Ro direnci haline getirebiliriz.Bunun için Rx direncinin uçlarındaki gerilimi ve bu gerilime seri direnci bulmamız gerekir.
Thevenin'in Eşdeğeri Devre no 1 de Rx direnci yokken Rx direnci uçlarındaki gerilim Vo gerilimidir. V1 - V2 = 120 - 80 = 40 volt kaynak gerilimi R1, R2, R3, R4 dirençleri üzerinden akar.Ohm kanununa göre V = I x R olduğu için, 40 V = 10 Ohm x İ amper olur buradan İ = 4 amper bulunur. R3 ve R1 dirençlerinde aynı formülden: V = 4 x (3+2) = 20 volt düşer ve 120 - 20 = 100 Volt gerilim Rx uçlarında kalır. Bu Eşdeğer devrenin Vo voltajıdır. Rx uçlarından görülen eşdeğer Ro direnci ise iki paralel bağlı (3+2) Ohmluk dirence eştir. Ro = 2.5 Ohm olur. Eşdeğer devrede Vo = 100 Volt Ro = 2.5 Ohm ve üzerinden geçen akımı bilmek istediğimiz Rx direnci ise 17.5 Ohm olduğu için; V = İ x R den 100 = İ x ( 17.5 + 2.5) İ = 100/20 =5 amper olur.
Özetle:
Thevenin eşdeğer devresini bulmak için.
1. Gerilim kaynakları kısa devre sayılır,istenen noktayı gören direnç eşdeğer dirençtir.
2. Devre akımı hesaplanır ve bu akıma göre Rx uçlarındaki voltaj bulunur. Bu eşdeğer kaynak gerilimidir.
NORTON TEOREMİ
Doğrusal bir devre, herhangi iki noktasına göre, bir akım kaynağı ve buna paralel bir direnç haline getirilebilir." Bunun için
1.Herhangi iki nokta uçları kısa devre iken geçen akım kaynak akımıdır
2. Gerilim kaynağı kısa devre iken, iki nokta arası direnç eşdeğer dirençtir.
Daha önce incelediğimiz devreyi ele alalım ve Norton eşdeğerini elde edelim. Gerilim kaynaklarını kısa devre ederek Thevenin teoremine benzer olarak
A B noktasını gören eşdeğer direnci bulalım. V1 ve V2 kaynakları kısa devre edilirse AB noktasını gören birbirine paralel iki adet 5 Ohm luk direnç olur ( 3 Ohm +2 Ohm). Bunların toplam değeri de 2.5 Ohm dur. Eşdeğer Ro direnci = 2.5 ohm olur. AB noktaları kısa devre edildiğinde AB den akan İk akımı: İ = V / R kullanılarak İk = İ1+İ2 İ1 = 120/5 = 24 Amper İ2 = 80/5 = 16 Amper İk = 24+16 = 40 Amper olur Ao eşdeğer Akım kaynağı 40 Amper,Ro eşdeğer direnç 2.5 Ohm dur.
O Halde AB noktasında Rx den geçen akım:yani İ Rx İ Rx = 40 x { Ro / Ro +R } olur İ Rx = 40 x { 2.5/ 17.5+2.5 } İ Rx = 40 x { 2.5 / 20 } İ Rx = 5 Amper olur.
İzleyiciler
TIMING CALCULATORS FOR THE LM555
TIMING CALCULATORS FOR THE LM555
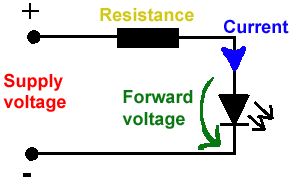
LED DİRENÇ HESAPLAMA
All LEDs require current limiting, without a current limiting mechanism the LED will usually burn out in under a second. Adding a simple resistor is the easiest way to limit the current. Use the calculator below to find out the value of resistor you require.
For example if you are wanting to power one of our_blank">red LEDs in an automotive application you would see that the typical forward voltage is 2.0 Volts and the maximum continuous forward current is 30mA. Therefore you would enter 14.5, 2.0 and 30 into the Single LED calculation box. After calculating you get 470ohm 1 watt as the result. Here is a that allows you to enter a resistor value and generate the corresponding color code.
Note: For automotive applications use the actual system voltage, not 12 Volts. Most 12 Volt system actually operate at around 14.5 Volts.
| Lm317 uygulama devreleri ve detayli bilgiye Buradan ulasabilirsiniz |
LM555 - ASTABLE OSCILLATOR CALCULATOR
NOTE: The leakage currents of electrolytic capacitors will affect the actual output results of the timers. To compensate for leakage it is often better to use a higher value capacitor and lower value resistances in the timer circuits.
LM555 Astable Oscillator Circuit Diagram
The next calculator can find the capacitance needed for a particular output frequency if the values of R1 and R2 are known.
| Value Of R1 Ohms | Value Of R2 Ohms |
| Frequency Desired Hertz |
|
| |
|
VOLT AMPER OHM ve WATT HESAPLAMA




Hiç yorum yok:
Yorum Gönder